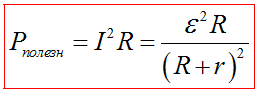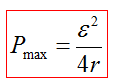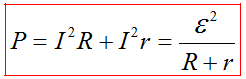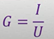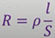Загрузка...Реостаты. Виды и устройство. Работа и особенности
Реостаты. Виды и устройство. Работа и особенности
Во многих электронных устройствах для регулирования громкости звука необходимо изменять силу тока. Рассмотрим устройство (реостаты), с помощью которого можно изменять силу тока и напряжение. Сила тока зависит от напряжения на концах участка цепи и от сопротивления проводника: I=U/R. Если изменять сопротивление проводника R, тогда будет меняться сила тока.
Сопротивление зависит от длины L, от площади поперечного сечения S и от материала проводника – удельного сопротивления. Для того чтобы изменять сопротивление проводника, нужно менять длину, толщину или материал. Весьма удобно изменять длину проводника.
Например, цепь, состоящая из источника тока, ключа, амперметра и проводника в виде резистора АС из проволоки с большим удельным сопротивлением.
Перемещая контакт С по этой проволоке, можно менять длину проводника, которая задействована в цепи, тем самым изменять сопротивление, а значит, и силу тока. Следовательно, можно создать устройство с переменным сопротивлением, с помощью которого можно изменять силу тока. Такие устройства имеют название реостатами.
Реостат – это устройство с изменяемым сопротивлением, которое служит для регулировки силы тока и напряжения.
Силу тока в цепи можно регулировать
Шотландский физик Роберт Уотсон-Уотт однажды был остановлен полицейским за превышение скорости, после чего сказал: «Если бы я знал, что вы будете с ним делать, то никогда не изобрел бы радар!».
—>СТАТИСТИКА —>
—>МЫ ВКОНТАКТЕ —>
—>НЕМНОГО РЕКЛАМЫ —>
Наши спонсоры
На практике часто приходится менять силу тока в цепи, делая ее то больше, то меньше. Так, изменяя силу тока в динамике радиоприемника, мы регулируем громкость звука. Изменением силы тока в электродвигателе швейной машины можно регулировать скорость его вращения.
Во многих случаях для регулирования силы тока в цепи применяют специальные приборы — реостаты.
Простейшим реостатом может служить проволока из материала с большим удельным сопротивлением, например, никелиновая или нихромовая. Включив такую проволочку в цепь источника электрического тока через контакты А и С и передвигая подвижный контакт С, можно уменьшать или увеличивать длину включенного в цепь участка АС. При этом будет меняться сопротивление цепи, а, следовательно, и сила тока в ней, это покажет амперметр.
Реостатам, применяемым на практике, придают более удобную и компактную форму. Для этой цели используют проволоку с большим удельным сопротивлением, а для того чтобы длинная проволока не мешала ее наматывают спиралью.
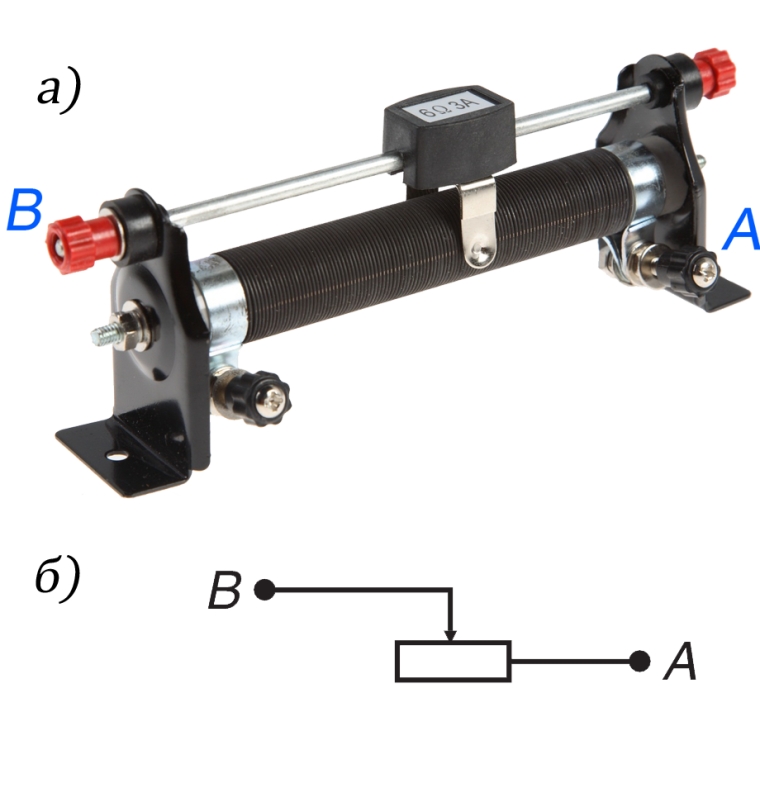
Один из реостатов (ползунковый реостат) изображен на рисунке а), а его условное обозначение в схемах — на рисунке б).
В этом реостате никелиновая проволока намотана на керамический цилиндр. Над обмоткой расположен металлический стержень, по которому может перемещаться ползунок. Своими контактами он прижат к виткам обмотки.
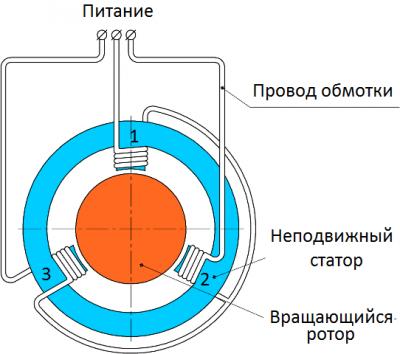
Электрический ток в цепи проходит от витков проволоки к ползунку, а через него в стержень, имеющий на конце зажим 1. С помощью этого зажима и зажима 2, соединенного с одним из концов обмотки и расположенного на корпусе реостата, реостат подсоединяют в цепь.
Стрелками указано как протекает электрический ток через реостат
Перемещая ползунок по стержню, можно увеличивать или уменьшать сопротивление реостата, включенного в цепь. То есть мы увеличиваем или уменьшаем количество витков по которым протекает электрический ток (чем больше витков, тем больше сопротивление).
Каждый реостат рассчитан на определенное сопротивление (чем больше проволоки намотано, тем большее сопротивление может дать такой реостат) и на наибольшую допустимую силу тока, превышать которую не следует, так как обмотка реостата накаляется и может перегореть. Сопротивление реостата и наибольшее допустимое значение силы тока указаны на реостате (см. рисунок а).
[Значения 6Ω и 3 А означают что данный реостат способен изменять свое сопротивление с 0 до 6 Ом, и ток с силой больше чем 3 Ампера пропускать по нему не стоит.]
Теперь самое время перейти от теории к практике!
Часть 1. Регулировка силы тока в лампочке.
На видео видно, как передвигая ползунок реостата вправо и влево, лампочка горит ярче или тусклее.
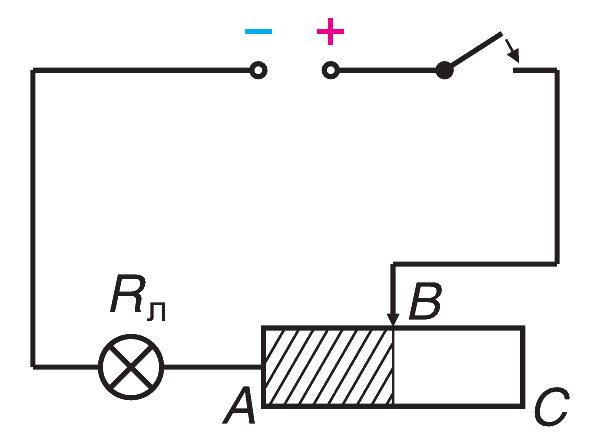
Понять принцип опыта можно взглянув на схему (см. рисунок 4).
На рисунке указана схема цепи, которую мы собирали в видео. Полное сопротивление цепи состоит из сопротивления Rл лампочки и сопротивления включенной в цепь части проволоки (на рисунке заштрихована) реостата. Незаштрихованная часть проволоки в цепь не включена. Если изменить положение ползунка, то изменится длина включенной в цепь части проволоки, что приведет к изменению силы тока.
Так, если передвинуть ползунок в крайнее правое положение (точка С), то в цепь будет включена вся проволока, сопротивление цепи станет наибольшим, а сила тока — наименьшей, поэтому нить лампочки будет гореть тускло или совсем не будет гореть (так как эл. ток такой силы не может разогреть спираль лампочки до свечения).
Если же передвинуть ползунок реостата в положение А, то электрический ток совсем не будет идти по проволоке реостата и, следовательно, сопротивление реостата будет равно нулю. Весь ток будет расходоваться на горение лампы, и она будет светить максимально ярко.
Часть 2. Включение лампочки от карманного фонаря в сеть 220 В.
Внимание! Не повторяйте этот опыт самостоятельно. Напоминаем, что поражение электрическим током осветительной сети может привести к смерти.
Что произойдет, если включить лампочку от фонарика в осветительную сеть напряжением 220 В? Понятно, что лампочка, рассчитанная на работу от батареек с суммарным напряжением 3,5 Вольт (3 пальчиковых батарейки), не способна выдержать напряжение в 63 раза большее – она сразу перегорит (может и взорваться).
Как тогда это сделать? На помощь придет уже известный нам прибор – реостат.
Нам нужен такой реостат, который способен был задержать бурный поток электрического тока, идущего от осветительной сети, и превратить его в тоненький ручеек электричества, который будет питать нашу хрупкую лампочку не нанося ей вреда.
Мы взяли реостат с сопротивлением 1000 (Ом). Это значит, что если эл. ток будет проходить по всей проволоке этого реостата, то на выходе из него получится ток с силой всего лишь 0,22 Ампер.
I=U/R=220 В / 1000 (Ом) = 0, 22 А
Для питания же нашей лампочки нужно даже более сильное электричество (0,28 А). То есть реостат не пропустит достаточное количество тока, чтобы зажечь нашу маленькую лампочку.
Это мы и наблюдаем во второй части видео, где в крайнем положении ползунка лампочка не горит, а при передвижении его вправо лампочка начинает загораться все ярче и ярче (подвигая ползунок мы запускаем все больше тока).
В определенный момент (на определенном положении ползунка реостата) лампочка перегорает, потому что реостат (при данном положении ползунка) пропустил слишком много электричества, которое и пережгло нить накаливания лампочки.
Так можно ли включить низковольтную лампочку в осветительную сеть? Можно! Только следует задержать все лишнее электричество реостатом с достаточно большим сопротивлением.
Часть 3. Включение лампы на 3,5 В вместе с лампой 60 Вт в сеть 220 В.
Мы взяли лампу мощностью 60 Вт, рассчитанную на напряжение 220 В, и лампочку от карманного фонарика на 3,5 В и силу тока 0,28 А.
Что произойдет, если включить эти лампочки в осветительную сеть напряжением 220 В? Понятно, что 60-ти ваттная лампочка будет гореть нормально (она на это и предназначена), а вот лампочка от карманного фонарика немедленно перегорит при включении ее в сеть (т.к. рассчитана работать от батареек только на 3,5 Вольта).
Но в опыте видно, как при подключении лампочек друг за другом (последовательно) и включении их в сеть 220 В обе лампы горят нормальным накалом и даже не думают перегорать. Даже когда ползунок реостата в крайнем положении (т.е. он не создает никакого сопротивления току) маленькая лампочка не перегорает.
Почему так? Почему даже при выключенном реостате (при его нулевом сопротивлении) лампа не перегорает? Что не дает ей перегореть при таком большом напряжении? И действительно ли напряжение на маленькой лампочке такое большое? Будет ли работать маленькая лампа если заменить лампу мощностью 60 Вт на стоваттную лампочку (100 Вт)?
Вы уже сможете ответить на большинство вопросов, если внимательно следили за ходом рассуждений в предыдущей части статьи. В этом опыте маленькой лампочке не дает перегорать большая лампочка. Она выступает в роли реостата с большим сопротивлением и берет на себя почти всю нагрузку.
Давайте попробуем разобраться как такое может происходить, что маленькая лампочка не перегорает благодаря лампочке в 60 Вт и доказать расчетным методом, что для нормального накала обеих лампочек необходимо одна и та же сила тока.
На помощь в решении этого вопроса нам придет физика, а конкретно ее раздел электричество (изучается в 8 классе).
Эксперимент № 3: Сравнение количеств теплоты при смешивании воды разной температуры
Внутренняя энергия тела может изменяться как путём совершения работы, так и путём теплопередачи (без совершения работы). Если изменение внутренней энергии происходит путём теплопередачи, то переход энергии от одних тел к другим осуществляется теплопроводностью, конвекцией или излучением.
Энергия, которую получает или теряет тело при теплопередаче, называется количеством теплоты.
Измерять количество теплоты учёные стали задолго до того, как в физике появилось понятие энергии. Тогда была установлена особая единица для измерения количества теплоты — калория (кал) или килокалория (ккал).
На практике часто пользуются тепловыми расчётами. Например, при строительстве зданий необходимо учитывать, какое количество теплоты должна отдавать зданию вся система отопления. Следует также знать, какое количество теплоты будет уходить в окружающее пространство через окна, стены, двери.
Гипотеза работы: если теплопередача происходит только между двумя телами, то согласно закону сохранения энергии количество теплоты, которое отдает более нагретое тело, равно количеству теплоты, которое получает менее нагретое тело.
В соответствии с гипотезой можно сформулировать цель работы: определить количество теплоты, отданное горячей водой и полученное холодной при теплообмене, и объяснить полученный результат.
Для выполнения эксперимента мне необходимы следующие приборы и материалы: калориметр, измерительный цилиндр (мензурка), термометр, стакан.
При выполнении опыта необходимо соблюдать технику безопасности:
- Необходимо аккуратно обращаться с сосудами, наполненными водой, со стеклянной посудой.
- Если сосуд разбит в процессе работы, то осколки нельзя убирать со стола тряпкой или руками, надо пользоваться щеткой и совком.
- Необходимо аккуратно обращаться с термометрами не встряхивать их.
- Осторожно обращаться с калориметром с горячей водой.
Нальем в калориметр горячую воду массой 100 г, а в стакан — столько же холодной и измерим температуру холодной и горячей воды.
Горячую воду нужно наливать во внутренний сосуд калориметра, вставленный во внешний сосуд.
Далее осторожно вольем холодную воду в сосуд с горячей водой, помешаем термометром полученную смесь и измерим её температуру.
Теперь можно рассчитать количество теплоты, отданное горячей водой при остывании до температуры смеси, и количество теплоты, полученное холодной водой при её нагревании до этой же температуры.
Откуда вообще появилось понятие переменный ток? к содержанию
Да с тех самых пор, когда человечество, узнав, что перемещение магнита вблизи проводника вызывает электрический ток в проводнике. Именно движение магнита вызывает ток, если магнит положить рядом с проводом и не двигать – никакого тока в проводнике это не вызовет. Далее, мы хотим получить (генерировать) в проводнике ток, чтобы использовать его в дальнейшем для каких-либо целей. Для этого изготовим катушку из медного провода и начнём возле неё двигать магнит. Магнит можно передвигать возле катушки как угодно – двигать по прямой туда-сюда, но, чтобы не двигать магнит руками, создать такой механизм технически сложнее, чем просто начать его вращать около катушки, аналогично вращению бутылки с водой из предыдущего примера. Вот именно таким образом — по техническим причинам — мы и получили синусоидальный переменный ток, используемый ныне повсеместно. Синусоида – это развёрнутое во времени описание вращения.
В дальнейшем оказалось, что законы протекания переменного тока в цепи отличаются от протекания постоянного тока. Например, для протекания постоянного тока сопротивление катушки равно просто омическому сопротивлению проводов. А для переменного тока – сопротивление катушки из проводов значительно увеличивается из-за появления, так называемого индуктивного сопротивления. Постоянный ток через заряженный конденсатор не проходит, для него конденсатор – разрыв цепи. А переменный ток способен свободно протекать через конденсатор с некоторым сопротивлением. Далее выяснилось, что переменный ток может быть преобразован с помощью трансформаторов в переменный ток с другими напряжением или силой тока. Постоянный ток такой трансформации не поддаётся и, если мы включим любой трансформатор в сеть постоянного тока (что делать категорически нельзя), то он неизбежно сгорит, так как постоянному току будет сопротивляться только омическое сопротивление провода, которое делается как можно меньше, и через первичную обмотку потечёт большой ток в режиме короткого замыкания.
Заметим также, что электродвигатели могут быть созданы для работы и от постоянного тока, и от переменного тока. Но разница между ними такая – электродвигатели постоянного тока сложнее в изготовлении, но зато позволяют плавно изменять скорость вращения обычным регулирующим силу тока реостатом. А электродвигатели переменного тока гораздо проще и дешевле в изготовлении, но вращаются только с одной, обусловленной конструкцией скоростью. Поэтому в практике широко применяются и те, и другие. В зависимости от назначения. Для целей управления и регулирования применяются двигатели постоянного тока, а в качестве силовых установок – двигатели переменного тока.
Далее конструкторская мысль изобретателя генератора двигалась примерно в таком направлении – если удобнее всего для генерации тока использовать вращение магнита рядом с катушкой, то почему бы вместо одной катушки генератора не расположить вокруг вращающегося магнита несколько катушек (места-то вокруг вон сколько)?
Получится сразу же, как бы несколько генераторов, работающих от одного вращающегося магнита. Причём переменный ток в катушках будет отличаться по фазе – максимум тока в последующих катушках будет несколько запаздывать относительно предыдущих. То есть синусоиды тока, если их графически изобразить, будут, как бы между собой, сдвинуты. Это важное свойство – сдвиг фаз, о котором мы расскажем ниже.
(Число катушек (фаз) вообще-то может быть любым, но для получения всех тех преимуществ, что даёт многофазная система генерации тока, минимально достаточно трёх).
Далее русский учёный электротехник Михаил Осипович Доливо-Добровольский развил изобретение Н. Тесла, впервые предложив трёх — и четырёхпроводную систему передачи трёхфазного переменного тока. Он предложил соединить один конец всех трёх обмоток генератора в одну точку и передавать электроэнергию всего по четырём проводам. (Экономия на дорогих цветных металлах существенная). Оказалось, что при симметричной нагрузке каждой фазы (равным сопротивлением) ток в этом общем проводе равняется нулю. Потому что при суммировании (алгебраическом, с учётом знаков) сдвинутых по фазе на 120 градусов токов они взаимно уничтожаются. Этот общий провод так и назвали – нулевой. Поскольку ток в нём возникает только при неравномерности нагрузок фаз и численно он небольшой, гораздо меньше фазных токов, то представилась возможность использовать в качестве «нулевого» провод меньшего сечения, чем для фазных проводов.
По этой же самой причине (сдвиг фаз на 120 градусов) трехфазные трансформаторы получились значительно менее материалоёмкими, так как в магнитопроводе трансформатора происходит взаимопоглощение магнитных потоков и его можно делать с меньшим сечением.
Сегодня трёхфазная система электроснабжения осуществляется четырьмя проводами, три из них называются фазными и обозначаются латинскими буквами: на генераторе — А, В и С, у потребителя — L1, L2 и L3. Нулевой провод так и обозначается – 0.
Напряжение между нулевым проводом и любым из фазных проводов называется – фазным и составляет в сетях потребителей – 220 вольт.
Между фазными проводами тоже существует напряжение, причём значительно выше, чем фазное напряжение. Это напряжение называется линейным и составляет в цепях потребителей 380 вольт. Почему же оно больше фазного? Да всё это из-за сдвига фаз на 120 градусов. Поэтому, если на одном проводе, к примеру, в данный момент времени потенциал равен плюс 200 вольт, то на другом фазном проводе в этот же момент времени потенциал будет минус 180 вольт. Напряжение – это разность потенциалов, то есть оно будет + 200 – (-180)=+380 В.
Возникает вопрос, если по нулевому проводу ток не протекает, то нельзя ли его вообще убрать. Можно. И мы получим трёхпроводную систему электроснабжения. С соединением потребителей так называемым «треугольником» — между фазными проводами. Однако нужно заметить, что при неравномерной нагрузке в сторонах «треугольника» на генератор будут действовать разрушающие его нагрузки, поэтому данную систему можно применять при огромном количестве потребителей, когда неравномерности нагрузок нивелируются. Передача электроэнергии от больших электростанций при высоких фазных и линейных напряжениях (сотни тысяч вольт) так и осуществляются. Почему же применяется такое высокое напряжение. Ответ простой – чтобы уменьшить потери в проводах на нагрев. Так как нагрев проводов (потери энергии) пропорционален квадрату протекающего тока, то желательно чтобы протекающий ток был минимален. Ну а для передачи необходимой мощности при минимальном токе нужно повышать напряжение. Линии электропередач (ЛЭП) так и обозначаются, к примеру, ЛЭП – 500 – это линия электропередачи под напряжением 500 киловольт.
Кстати потери в проводах ЛЭП можно ещё более снизить, применяя передачу постоянного тока высокого напряжения (перестаёт действовать емкостная составляющая потерь, действующая между проводами), проводились даже такие эксперименты, но широкого распространения пока такая система не получила, видимо вследствие большей экономии в проводах при трёхфазной системе генерации.
Коэффициент полезного действия
Мощность, выделяемая на внешнем участке цепи, называется полезной
При условии R=r мощность, выделяемая во внешней цепи, максимальная для данного источника и равна
Полная мощность — сумма полезной и теряемой мощности
Коэффициент полезного действия источника тока — отношение полезной мощности к полной
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Закон Ома для участка цепи. Сопротивление»
На прошлом уроке мы с вами говорили об электрическом токе и его действиях. Очевидно, что различные действия тока зависят от силы протекающего тока. Напомним, что силой тока мы с вами назвали физическую величину, численно равную заряду, прошедшему через поперечное сечение проводника за единицу времени.
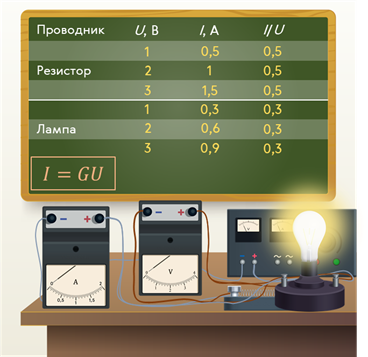
Таким образом, регулировать действия тока можно изменяя силу тока. Но для того чтобы получить возможность управлять током в цепи, нужно знать, от чего и как он зависит. Для установления этой зависимости возьмём резистор, который подключим в цепь с источником тока, выходное напряжение между клеммами которого можно регулировать. С помощью последовательно включённого амперметра и параллельно резистору вольтметра будем измерять силу тока и напряжение на спирали резистора.
Меняя выходное напряжение в целое число раз, мы заметим, что изменяется и ток в цепи, и напряжение на концах проводника. При этом во сколько раз увеличивается напряжение на концах данного проводника, во столько же раз увеличивается и ток в нём.
Если взять другой проводник и повторить с ним те же самые опыты, то мы увидим, что ток и в этом проводнике строго пропорционален напряжению на концах проводника.
Обозначая напряжение на концах проводника через U, а ток — через I, можно записать, что сила тока в проводнике прямо пропорциональна приложенному напряжению:
I = GU.
В этой формуле величина G зависит от свойств проводника: чем больше G тем больше и ток в проводнике при одном и том же напряжении. Но для данного проводника при всех значениях тока и напряжения величина этого коэффициента остаётся постоянной и равной отношению силы тока к напряжению (при условии, что температура проводника не меняется):
Следовательно, данная величина характеризует свойство данного проводника. Её назвали электропроводностью или просто проводимостью проводника. Единица электропроводности в Си названа сименсом (См), в честь немецкого учёного и предпринимателя Вернера фон Сименса.
Величина, обратная проводимости, называется сопротивлением проводника.
Давайте вспомним, что электрическое сопротивление — это скалярная физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока в нём.
Выражая в предыдущей формуле проводимость через сопротивление, получаем, что сила тока в данном участке цепи, прямо пропорциональна напряжению на этом участке и обратно пропорциональна его сопротивлению.
Этот закон впервые был открыт в тысяча восемьсот двадцать шестом (1826) году немецким учёным Генри Омом и называется законом Ома для участка цепи.
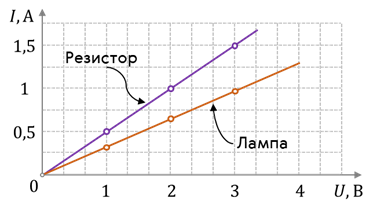
Как и всякую закономерность, закон Ома можно представить графически в виде так называемой вольт-амперной характеристики проводника, то есть зависимости силы тока в проводнике от напряжения на его концах.
Как видим, график подтверждает прямую пропорциональную зависимость силы тока в проводнике от приложенного к нему напряжения.
Зная величину напряжения на концах проводника и ток в нём, по закону Ома можно вычислить сопротивление проводника, как отношение напряжения на концах проводника к силе тока в проводнике:
Из этой формулы можно вывести единицу сопротивления. Итак, за единицу сопротивления принимают сопротивление такого проводника, по которому проходит ток 1 А при напряжении на концах проводника 1 В. Эта единица сопротивления называется омом.
Для измерения сопротивления проводников необходимо было прежде всего выбрать образец, или, как принято называть, эталон сопротивления. В 1860 году Вернер Сименс предложил в качестве эталона ома принять сопротивление столбика ртути длиной 106,3 см, имеющего по всей длине постоянное сечение, равное 1 мм 2 , при температуре таяния льда.
В 1908 году Международный съезд электриков в Лондоне одобрил этот эталон и назвал его международным омом.
Стандарт ртутного столба применялся вплоть до 1948 года. В этом году на Генеральной конференции по мерам и весам ом был переопределён в абсолютном выражении, а не как стандарт эталона.
Следует отметить, что один ом — это достаточно маленькое сопротивление. Даже у спиралей обычных электроламп оно составляет сотни ом. Поэтому часто сопротивление выражают в килоомах (1 кОм = 10 3 Ом) и мегаомах (1 МОм = 10 6 Ом).
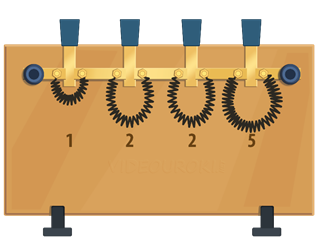
Набор образцовых сопротивлений, с которыми можно сравнивать измеряемые сопротивления, называется магазином сопротивлений. На рисунке вы видите устройство такого прибора.
В его верхней части имеется группа металлических пластин, которые можно соединять друг с другом вставляемыми между ними штырями. К пластинам подключены металлические спирали с определёнными сопротивлениями. Если прибор включён в цепь крайними клеммами и штыри между пластинами вынуты, то ток идёт последовательно через все спиральки. Вынимая тот или иной штырь или группу штырей, мы можем при помощи магазина получить различные сопротивления в зависимости от величины сопротивления спиралей, имеющихся в магазине.
Исходя из определения сопротивления кажется, что оно зависит от силы тока и напряжения. Однако это не так. Чтобы понять от чего зависит сопротивление проведём несколько простых опытов с панелью сопротивлений.
Итак, включим в цепь источника тока половинку верхнего провода и измерим амперметром ток в цепи. Теперь подключим весь провод. Мы замечаем, что ток в цепи становится слабее. Причём слабее почти в два раза. Если взять более толстую проволоку (в нашем случае — это два верхних провода, сложенных вместе), то, как видим, ток в цепи становится в два раза сильнее. Наконец подключим самую нижнюю проволоку, изготовленную из железа, размеры которой такие же, что и у самой верхней проволоки. Легко заметить, что при одном и том же напряжении по железной проволоке идёт значительно меньший ток. Следовательно, проводники одинаковых размеров, но изготовленные из различных материалов, обладают неодинаковым сопротивлением.
Обобщив результаты наших опытов, мы можем утверждать, что: сопротивление проводника прямо пропорционально его длине, обратно пропорционально площади поперечного сечения и зависит от вещества, из которого этот проводник изготовлен.
Сопротивление проводника зависит также от его температуры (но об этом в следующий раз).
Величина, обозначенная греческой буквой ρ, характеризует электрические свойства проводника. Она называется удельным сопротивлением проводника. Её численное значение зависит от единиц, в которых измерена длина и сечение проводника. В системе СИ единицей удельного сопротивления служит ом-метр, (Ом ∙ м).
Таким образом, удельное сопротивление проводника — скалярная физическая величина, численно равная сопротивлению однородного цилиндрического проводника, изготовленного из данного вещества и имеющего длину 1 м и площадь поперечного сечения 1 м 2 (или сопротивлению куба с ребром 1 м).
В приводимой таблице указаны удельные сопротивления проводников для некоторых веществ при температуре 20 °С.
Наименьшим удельным сопротивлением, как видно из таблицы, обладают химически чистые серебро и медь. Металлические сплавы имеют значительно большее удельное сопротивление, чем чистые металлы, из которых состоят эти сплавы. А удельные сопротивления диэлектриков просто огромны.
В настоящее время большое применение в технике находят твёрдые вещества, механизм электрической проводимости у которых иной, чем у металлов, электролитов и газов. Такие вещества называются полупроводниками (но о них мы с вами будем говорить в ближайшее время). А сейчас, для закрепления материала, решим с вами такую задачу. Предположим, что у нас есть два цилиндрических проводника из одного и того же металла, которые имеют одинаковую массу, но диаметр второго проводника в 3 раза больше, чем первого. Во сколько раз будут отличаться силы тока в проводниках, если их подключить к одинаковым источникам тока?
